
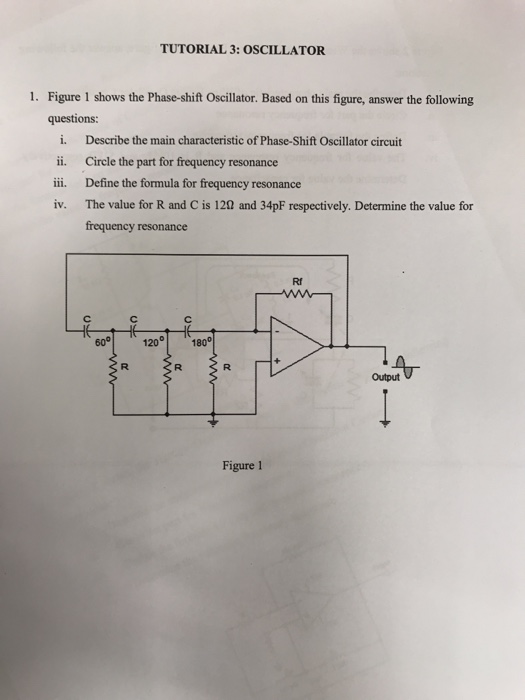
In particular, the analytical expressions characterizing various half-return maps associated with the Poincare map are used in a crucial way to prove the existence of a Shilnikov-type homoclinic orbit, thereby establishing rigorously the chaotic nature of the double scroll. Analytical expressions for various Poincare maps are then derived and used to characterize the birth and the death of the double scroll, as well as to derive an approximate one-dimensional map in analytic form which is useful for further bifurcation analysis. An explicit normal-form equation in the context of global bifurcation is derived and parameterized by their eigenvalues.
In the special case in which they are identical, one has exact equivalence in the sense of linear conjugacy. A necessary and sufficient condition for two such piecewise-linear vector fields to be linearly equivalent is that their respective eigenvalues be a scaled version of each other. The approach is to derive a linearly equivalent class of piecewise-linear differential equations which includes the double scroll as a special case. The authors provide a rigorous mathematical proof that the double scroll is chaotic.

Moreover, a comparative study with a sample of existing chaotic NRO/NCO schemes, show that the proposed class of chaotic NRO/NCO is optimal since it provides minimum building constituents and lower dynamic order, while offering a new palette of chaotic attractors with great topological strangeness. Therefore, new strange chaotic attractors with 2D/3D shapes are created and presented.

Then, despite the simplicity of the 2 nd order NRO/NCO, a relevant parameterization strategy associated with virtual simulation techniques, are used as key exploration means for creating relevant chaotic phenomena. The feasibility of relevant chaotic phenomena is proven from the existence of their Van Der Pol dynamic models according to the least square estimation principle. Compared to most chaotic electronic schemes encountered in nonlinear dynamic systems theory and practice, the proposed class of chaotic circuits consists of simple piecewise linear NRO/NCO, involving a minimum number of building components and dynamic states. In this paper, the chaotic phenomena are outlined in a class of simple NRO (negative resistance oscillator) or NCO (negative conductance oscillator) equivalently. The structural stability of strange attractors observed numerically was finally proved via a real practical experiment: a flow-equivalent chaotic oscillator was constructed as the lumped electronic circuit, and desired attractors were captured and provided as oscilloscope screenshots. Chaotic and hyperchaotic behavior were deeply analyzed by using standard numerical tools such as Lyapunov exponents, basins of attraction, bifurcation diagrams, and solution sensitivity. Both cases cause vector field symmetry and allow the coexistence of several different attractors. For starters, the two-port that represents the transistor was firstly assumed to have a polynomial-forward trans-conductance then the shape of trans-conductance changes into the piecewise-linear characteristics. By considering the generalized bipolar transistor as an active element and after applying the search-for-chaos optimization approach, parameter regions that lead to either chaotic or hyperchaotic dynamics were discovered. This paper describes recent findings achieved during a numerical investigation of the circuit known as the Clapp oscillator.


 0 kommentar(er)
0 kommentar(er)
